Yilin Mo

I am an Associate Professor at Tsinghua University, China.

© 2022. All rights reserved.

Model Reference Adaptive Control

01 Sep 2015

Consider the following first-order linear system:

\begin{equation} \dot{x} = a x + bu, \label{eq:truesystem} \end{equation}

where \(a,\,b\) are unknown parameters. However, the sign of \(b\) is known.

Suppose that we want the linear system \eqref{eq:truesystem} to track the following reference system:

\begin{equation} \dot{x_m} = a_m x_m + b_m r, \label{eq:refsystem} \end{equation}

where \(a_m < 0\) and \(b_m\) are known and \(r(t)\) is a known reference signal.

Suppose we use the following control law:

\begin{equation} u = \hat k_x x + \hat k_r r. \end{equation}

Then the dynamic of system \eqref{eq:truesystem} will be

\begin{equation} \dot{x} = (a + b \hat k_x) x + b \hat k_r r. \end{equation}

Therefore, if we can make

\begin{equation} \hat k_x = k_x \triangleq \frac{a_m-a}{b}\text{ and }\hat k_r = k_r \triangleq \frac{b_m}{b}, \end{equation}

then the dynamic of system \eqref{eq:truesystem} will follow the reference system. Let us denote \(\Delta k_x \triangleq k_x - \hat k_x\) and \(\Delta k_r \triangleq k_r - \hat k_r\).

Now consider the dynamic of the error \(e \triangleq x - x_m\), we have

\begin{align*} \dot{e}& = (a + b \hat k_x) x + b \hat k_r r - a_m x_m - b_m r\\ & = a_m(x - x_m) - b \Delta k_x x - b \Delta k_r r \\ & = a_m e - b \Delta k_x x - b \Delta k_r r . \end{align*}

Therefore, if we consider the following candidate Lyapunov function

\begin{equation} V = \frac{1}{2}\left(e^2 + |b|(\gamma_x^{-1} \Delta k_x^2 + \gamma_r^{-1} \Delta k_r^2)\right), \end{equation}

where \(\gamma_x,\,\gamma_r > 0\). Then we have

\begin{align*} \dot{V} = a_m e^2 &- |b|\Delta k_x \left(\text{sgn}(b)ex + \gamma_x^{-1}\dot{\hat k_x}\right) \\ &- |b|\Delta k_r \left(\text{sgn}(b)er + \gamma_r^{-1}\dot{\hat k_r}\right). \end{align*}

Therefore, if we use the following update rule on \(\hat k_x\) and \(\hat k_r\):

\begin{equation} \dot{\hat k_x} = -\gamma_x \text{sgn}(b) ex\text{ and }\dot{\hat k_r} = -\gamma_r \text{sgn}(b) er,\\ \end{equation}

then \(\dot{V} = a_m e^2 \leq 0\). One can then prove that \(\ddot{V} =2 a_m e \dot{e}\) is bounded and thus \(\lim_{t\rightarrow\infty} \dot{V} = 0\) and hence \(e \rightarrow 0\).

Simulation

Assume that the system is given as

\begin{equation} \dot{x} = x + u, \end{equation}

while we want the system to tract the following system:

\begin{equation} \dot{x_m} = - x_m + r = - x_m + \sin(t). \end{equation} 
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns # for the sake of appreances
from scipy.integrate import odeint

a = 1.
b = 1.
am = -1.
bm = 1.
gammax = 10.
gammar = 10.

# y is a vector of [x ,x_m, \hat k_x, \hat k_r]
def f(y, t):
    x = y[0]
    xm = y[1]
    hatkx = y[2]
    hatkr = y[3]
    r = np.sin(t)
    e = x - xm
    u = hatkx * x + hatkr * r
    f0 = a * x + b * u
    f1 = am * xm + bm * r
    f2 = -1 * gammax * e * x
    f3 = -1 * gammar * e * r
    return [f0, f1, f2, f3]

t = np.linspace(0, 20., 10000) 
x0 = 0.
xm0 = 0.
hatkx0 = 0.
hatkr0 = 0.
y0 = [x0, xm0, hatkx0, hatkr0]

solution = odeint(f, y0, t)

x = solution[:, 0]
xm = solution[:, 1]
hatkx = solution[:, 2]
hatkr = solution[:, 3]

fig = plt.figure()
plt.rc('text', usetex=True)
plt.plot(t, np.sin(t), label=r'$r(t)$')
plt.plot(t, x, label=r'$x(t)$')
plt.plot(t, xm, label=r'$x_m(t)$')
plt.plot(t, hatkx, label=r'$\hat k_x(t)$')
plt.plot(t, hatkr, label=r'$\hat k_r(t)$')
plt.xlabel('Time(t)')
plt.legend(loc = 0)
fig.tight_layout()
plt.savefig('../../public/mrac.png')
return '../../public/mrac.png' # return the filename to org-mode

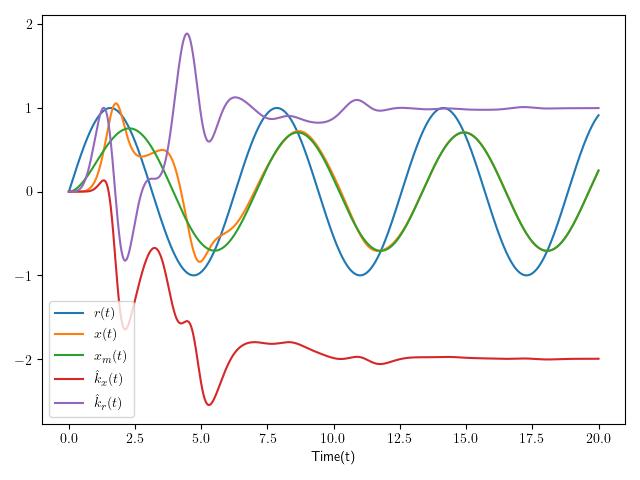
mrac.png

Figure 1: The simulation result for model reference adaptive control. Notice that \(e(t) = x(t) - x_m(t)\) converges to 0 and \(\hat k_x \rightarrow -2\) and \(\hat k_r \rightarrow 1\).

Related Posts